Determine Whether a Function is Continuous or Differentiable at Xc by Looking at a Graph
FIND THE DERIVATIVES FROM THE LEFT AND RIGHT AT THE GIVEN POINT
About "Find the Derivatives From the Left and Right at the Given Point"
Find the Derivatives From the Left and Right at the Given Point :
Here we are going to see how to check if the function is differentiable at the given point or not.
How to Find if the Function is Differentiable at the Point ? :
The function is differentiable from the left and right. As in the case of the existence of limits of a function at x0, it follows that
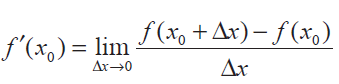
exists if and only if both
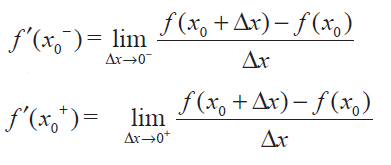
exist and f' (x0-) = f' (x0+)
Hence
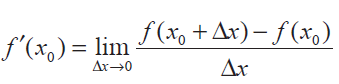
if and only if f' (x0-) = f' (x0+) . If any one of the condition fails then f'(x) is not differentiable at x0.
How to Know If a Function is Differentiable at a Point - Examples
Question 1 :
Determine whether the following function is differentiable at the indicated values.
(i) f(x) = x | x | at x = 0
Solution :
f(x) = x | x |
If x < 0, thenf(x) = x (-x) = -x 2
If x > 0, thenf(x) = x (x) = x 2
f'(0-) = lim x->0- [(f(x) - f(0)) / (x - 0)]
= limx->0- (-x2 - 0) / x
= limx->0- -x
= 0 -----(1)
f'(0+) = limx->0+ [(f(x) - f(0)) / (x - 0)]
= limx->0+ (x2 - 0) / x
= limx->0+ x
= 0 -----(2)
f'(0 - ) = f'(0 + )
Hence the given function is differentiable at the point x = 0.
(ii) f(x) = |x2 - 1| at x = 1
Solution :
f(x) = |x 2 - 1|
If x < 1, thenf(x) = -(x2 - 1)
If x > 1, then f(x) = (x 2 - 1)
f'(1-) = limx->1- [(f(x) - f(1)) / (x - 1)]
= limx->1- [(-x2 + 1) - (0)] / (x - 1)
= limx->1- [-(x2 - 1) / (x - 1)]
= limx->1- [-(x + 1)(x - 1) / (x - 1)]
= -2 -----(1)
f'(1+) = limx->1+ [(f(x) - f(1)) / (x - 1)]
= limx->1+ [(x2 - 1) - (0)] / (x - 1)
= limx->1+ [(x + 1)(x - 1) / (x - 1)]
= limx->1+ (x + 1)
= 2 -----(2)
f'(1 - ) ≠ f'(1 + )
Hence the given function is not differentiable at the point x = 1.
(iii) f(x) = |x| + |x - 1| at x = 0, 1
Solution :
f(x) =|x| + |x - 1|
Check if the given function is continuous at x = 0.
If x < 0, thenf(x) = -x - (x - 1)
f(x) = -x - x + 1
= -2x + 1
If x > 0 and x < 1 , thenf(x) =x - (x - 1)
f(x) = x - x + 1
= 1
If x > 1, thenf(x) =x + (x - 1)
f(x) = x + x + 1
= 2x + 1
f'(0 - ) = lim x->0- [(f(x) - f(0)) / (x - 0)]
= limx->0- [(-2x + 1) - 1] / x
= limx->0- -2x / x
= limx->0- -2
= -2 -----(1)
f'(0+) = limx->0+ [(f(x) - f(0)) / (x - 0)]
= limx->0+ [1 - 1] / x
= limx->0- 0 / x
= 0/0 -----(2)
f'(0 - ) ≠ f'(0 + )
f'(1 - ) = lim x->1- [(f(x) - f(1)) / (x - 1)]
= limx->1- [1 - 1] / (x - 1)
= limx->1- 0 / (x-1)
= 0 -----(1)
f'(1+) = limx->1+ [(f(x) - f(1)) / (x - 1)]
= limx->1+ [2x + 1 - 3] / (x - 1)
= limx->1+ (2x - 2) / (x - 1)
= limx->1+ 2(x - 1) / (x - 1)
= 2 -----(2)
f'(1 - ) ≠ f'(1 + )
Hence the given function is not differentiable at the given points.

After having gone through the stuff given above, we hope that the students would have understood, " How to Find if the Function is Differentiable at the Point"
Apart from the stuff given in " How to Find if the Function is Differentiable at the Point" , if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback tov4formath@gmail.com
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com
schoonoversibacted.blogspot.com
Source: https://www.onlinemath4all.com/how-to-find-if-the-function-is-differentiable-at-the-point.html
0 Response to "Determine Whether a Function is Continuous or Differentiable at Xc by Looking at a Graph"
Post a Comment